Rezultati ispitivanja mogu pomoći u postavljanju dijagnoze kod simptomatskih bolesnika (dijagnostičko testiranje) ili identificiranju okultne bolesti kod asimptomatskih bolesnika (probir). Međutim, rezultati ispitivanja mogu ometati donošenje kliničkih odluka ako test slabo razlikuje pacijente s i bez bolesti, ako rezultat nije u skladu s kliničkom slikom ili ako je rezultat ispitivanja nepravilno integriran u klinički kontekst.
Laboratorijski testovi su nesavršeni i mogu pogrešno identificirati neke zdrave ljude kao bolesne (lažno pozitivan rezultat) ili mogu pogrešno identificirati neke pogođene ljude kao slobodne od bolesti (lažno negativan rezultat). Sposobnost testa da ispravno identificira bolesnike s bolešću ovisi o vjerojatnosti da će osoba imati bolest (prethodna vjerojatnost) i o unutrašnjim radnim karakteristikama testa.
Iako je dijagnostičko testiranje često presudno u donošenju kliničkih odluka, ispitivanje može imati neželjene ili nenamjerne posljedice. Ispitivanje se mora vršiti s namjerom i s očekivanjem da će rezultat testa smanjiti nejasnoće oko bolesnikovih problema i doprinijeti njihovom zdravlju. Osim rizika od pružanja netočnih informacija (čime se odlaže započinjanje liječenja ili izaziva nepotrebno liječenje), laboratorijski testovi troše ograničene resurse i mogu sami imati štetne učinke (npr. pneumotoraks uzrokovan biopsijom pluća) ili mogu zahtijevati dodatna nepotrebna ispitivanja.
Definiranje pozitivnog rezultata testa
Među najčešćim testovima su oni koji daju rezultate u kontinuiranoj, kvantitativnoj ljestvici (npr. glukoza, leukociti). Takvi testovi mogu pružiti korisne kliničke informacije kroz njihov raspon, ali ih kliničari često koriste za dijagnosticiranje stanja zahtijevajući da se rezultat klasificira kao pozitivan ili negativan (tj. bolest prisutna ili odsutna) na temelju usporedbe s nekim utvrđenim kriterijem ili granicom prekida. Takve granične vrijednosti obično se biraju na temelju statističkih i konceptualnih analiza kojima se pokušava izbalansirati stopa lažno pozitivnih rezultata (poticanje nepotrebnih, skupih i eventualno opasnih testova ili liječenja) i lažno negativnih rezultata (ako se ne dijagnosticira bolest koja se liječi). Identificiranje granične vrijednosti također ovisi o zlatnom standardu za prepoznavanje dotične bolesti.
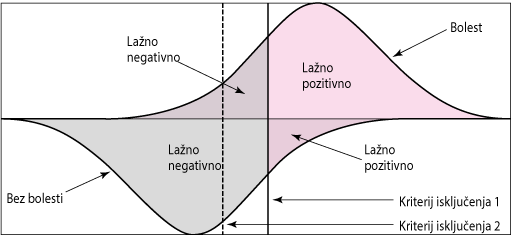
Tipično, kvantitativni rezultati ispitivanja (npr. leukociti u slučajevima sumnje na upala slijepog crijeva) obično prate neku vrstu krivulje raspodjele (ne nužno normalnu krivulju, iako se obično prikazuje kao takva). Raspodjela rezultata ispitivanja za bolesnike s bolešću usmjerena je na drugačiju točku od one za bolesnike koji nemaju bolest. Neki će bolesnici s bolešću imati vrlo visok ili vrlo nizak rezultat, ali većina ima rezultat usredotočen na srednju vrijednost. Suprotno tome, neki bolesnici bez bolesti imaju vrlo visok ili vrlo nizak rezultat, ali većina ima rezultat usredotočen na drugačiju vrijednost od one za bolesnike s bolešću. Za većinu testova, distribucije se preklapaju tako da se mnogi mogući rezultati ispitivanja javljaju kod pacijenata s i bez bolesti; takvi su rezultati jasnije prikazani kada su krivulje prikazane na istom grafu (vidjeti sliku). Neki će pacijenti iznad i ispod odabrane točke prekida biti pogrešno okarakterizirani. Podešavanje granične vrijednosti kako bi se identificiralo više pacijenata s bolešću (povećala osjetljivost na testove) također povećava broj lažno pozitivnih rezultata (loša specifičnost), a pomicanje granične vrijednosti na drugi način kako bi se izbjeglo lažno dijagnosticiranje pacijenata koji imaju bolest, povećava se broj lažno negativnih. Svaka granična točka povezana je s određenom vjerojatnošću stvarno-pozitivnih i lažno-pozitivnih rezultata.
Distribucija rezultata ispitivanja.
|
Pacijenti s bolesti prikazani su u gornjoj distribuciji; bolesnici bez bolesti prikazani su u nižoj distribuciji. Za bolesnike s bolešću, područje ispod raspodjele rezultata koja se nalazi desno od (iznad) kriterija presjeka odgovara stvarno pozitivnoj stopi testa (tj. njegovoj osjetljivosti); područje koje leži lijevo (dolje) od kriterija odgovara lažno negativnoj stopi. Za bolesnike bez bolesti, područje s desne strane kriterija isključivanja odgovara lažno pozitivnoj stopi, a područje s lijeve strane odgovara stvarno-negativnoj stopi (tj. njezinoj specifičnosti). Za dvije raspodjele preklapanja (npr. bolesnici s i bez bolesti) pomicanje linije kriterija rezanja utječe na osjetljivost i specifičnost, ali u suprotnim smjerovima; promjenom kriterija isključivanja s 1 na 2 smanjuje se broj lažno negativnih (povećava osjetljivost), ali također povećava i broj lažno pozitivnih rezultata (smanjuje se specifičnost).
|
Krivulje operativne karakteristike prijemnika (ROC)
Grafički udio stvarno pozitivnih rezultata (broj stvarno pozitivnih rezultata / broj s bolesti) i udjela lažno pozitivnih rezultata (broj lažno pozitivnih rezultata / broj bez bolesti) za niz presjeka generira ono što je poznato kao ROC krivulja. ROC krivulja grafički prikazuje razmjere između osjetljivosti i specifičnosti kada je podešena točka granične vrijednosti (vidi sliku Krivulja tipičnih operativnih karakteristika prijemnika (ROC)). Prema dogovoru, stvarno pozitivni ulomak je smješten na osi y, a lažno pozitivni ulomak postavljen na osi x. Što je veće područje ispod ROC krivulje, test bolje razlikuje pacijente s ili bez bolesti.
ROC krivulje omogućuju uspoređivanje testova za različite točke graničenja. U primjeru, test A djeluje bolje nego test B u svim rasponima. ROC krivulje također pomažu u odabiru točke isključivanja koja je dizajnirana kako bi se povećala korisnost testa. Ako je test namijenjen potvrđivanju bolesti, odabire se granična točka s većom specifičnošću i nižom osjetljivošću. Ako je test osmišljen za provjeru okultne bolesti, odabire se granična točka s većom osjetljivošću i nižim specifičnostima.
Tipična krivulja rada prijemnika (ROC).
Karakteristike testa
Neke kliničke varijable imaju samo dva moguća rezultata (npr. živ / mrtav, trudna / nije trudna); takve varijable nazivaju se kategoričkim i dihotomnim. Ostali kategorijski rezultati mogu imati mnogo diskretnih vrijednosti (npr. krvna grupa, Glasgow koma skala) i nazivaju se nominalnim ili rednim. Nominalne varijable poput krvne grupe nemaju određeni redoslijed. Ordinalne varijable poput Glasgow koma skale imaju diskretne vrijednosti raspoređene u određenom redoslijedu. Ostale kliničke varijable, uključujući mnoge tipične dijagnostičke testove, su kontinuirane i imaju beskonačan broj mogućih rezultata (npr. broj leukocita, razina glukoze u krvi). Mnogi kliničari odabiru graničnu točku koja može uzrokovati da se kontinuirana varijabla tretira kao dihotomska varijabla (npr. za bolesnike s razinom glukoze u krvi natašte > 126 mg / dL (7,0 mmol/L) smatra se da imaju dijabetes). Ostala kontinuirana dijagnostička ispitivanja imaju dijagnostičku korisnost kada imaju višestruke točke prekida ili ako rasponi rezultata imaju različitu dijagnostičku vrijednost.
Kada se rezultati ispitivanja mogu definirati kao pozitivni ili negativni, svi mogući ishodi mogu se zabilježiti u jednostavnoj tablici 2 × 2 (vidi tablicu Distribucija rezultata hipotetičkih ispitivanja) iz koje su važne diskriminatorne karakteristike ispitivanja, uključujući osjetljivost, specifičnost, pozitivne i negativne prediktivne vrijednosti, a omjer vjerojatnosti (LR) se može izračunati (vidjeti tablicu Raspodjela rezultata ispitivanja hipotetičkog testa esteraze leukocita u skupini od 1000 žena s pretpostavljenom 30% prevalencijom UTI).
Distribucija rezultata pretrage.
|
Rezultati
|
Bolest prisutna
|
Bolest odsutna
|
|
Test pozitivan
|
stvarno pozitivan
|
lažno pozitivan
|
|
Test negativan
|
lažno negativan
|
stvarno negativan
|
|
Ukupno bolesnika
|
Svi bolesnici s bolešću
|
Svi bolesnici bez bolesti
|
Osjetljivost, specifičnost i prediktivne vrijednosti
Vrijednosti osjetljivosti, specifičnosti i prediktivne vrijednosti obično se smatraju karakteristikama samog testa, neovisno o populaciji bolesnika.
Dakle, test koji je pozitivan kod 8 od 10 bolesnika s bolešću ima osjetljivost 0,8 (također izraženu kao 80%). Osjetljivost predstavlja koliko dobro test otkriva bolest; test s niskom osjetljivošću ne identificira mnoge bolesnike s bolešću, a test s visokom osjetljivošću je koristan za isključenje dijagnoze kada su rezultati negativni. Osjetljivost je dopuna lažno-negativne stope (tj. lažno-negativna stopa plus osjetljivost = 100%).
Dakle, test koji je negativan kod 9 od 10 bolesnika bez bolesti ima specifičnost 0,9 (ili 90%). Specifičnost predstavlja koliko dobro test pravilno identificira bolesnike s bolešću jer testovi s visokom specifičnošću imaju nisku lažno pozitivnu stopu. Test niske specifičnosti dijagnosticira mnoge bolesnike bez bolesti kao bolesne. To je dopuna lažno pozitivne stope.
Dakle, ako je 9 od 10 pozitivnih rezultata testa točno (stvarno pozitivno), PPV je 90%. Budući da svi pozitivni rezultati ispitivanja imaju određeni broj stvarno pozitivnih i nekih lažno pozitivnih rezultata, PPV opisuje koliko je vjerojatno da će pozitivni rezultati testa u određenoj populaciji bolesnika biti stvarno pozitivni.
Dakle, ako je 8 od 10 negativnih rezultata ispitivanja točno (stvarno negativno), NPV je 80%. Budući da nisu svi negativni rezultati ispitivanja stvarno negativni, neki bolesnici s negativnim rezultatom testa zapravo imaju bolest. NPV opisuje koliko je vjerojatno da je negativan rezultat testa u određenoj populaciji bolesnika stvarno negativan.
Omjer vjerojatnosti (LRS)
Za razliku od osjetljivosti i specifičnosti, koji se ne odnose na specifične vjerojatnosti bolesnika, LR omogućuje kliničarima da interpretiraju rezultate ispitivanja kod određenog bolesnika pod uvjetom da postoji poznata (iako često procijenjena) vjerojatnost bolesti prije ispitivanja.
LR opisuje promjenu vjerojatnosti bolesti prije testa kada je rezultat ispitivanja poznat i odgovara na pitanje: „Koliko se promijenila vjerojatnost nakon ispitivanja sada kada je poznat rezultat ispitivanja?“ Mnogi klinički testovi su dihotomni; oni su ili iznad točke presjeka (pozitivne) ili ispod granice presjeka (negativne) i postoje samo 2 moguća rezultata. Stvarna vjerojatnost nakon ispitivanja ovisi o veličini LR-a (koja ovisi o radnim karakteristikama testa) i procjeni vjerojatnosti pre-testa. Kad je test koji se radi je dihotoman, a rezultat pozitivan ili negativan, osjetljivost i specifičnost mogu se koristiti za izračunavanje pozitivnog LR (LR +) ) ili negativnog LR (LR-).
-
LR
+
: Omjer vjerojatnosti pozitivnog rezultata testa u bolesnika s bolešću (stvarno pozitivan) i vjerojatnosti pozitivnog rezultata testa u bolesnika bez bolesti (lažno pozitivan)
-
LR
-
: Omjer vjerojatnosti negativnog rezultata testa u bolesnika s bolešću (lažno negativan) i vjerojatnosti negativnog rezultata testa u bolesnika bez bolesti (stvarno negativan)
Kada je rezultat kontinuiran ili ima višestruke točke rezanja, ROC krivulja, a ne osjetljivost i specifičnost, koristi se za izračunavanje LR koji se više ne opisuje kao LR + ili LR-.
Kako je LR omjer međusobno isključivih događaja, a ne udio ukupnog, on predstavlja izglede umjesto vjerojatnosti. Za određeni test, LR je različit za pozitivne i negativne rezultate.
Na primjer, s obzirom na pozitivan rezultat testa, LR od 2,0 pokazuje da su šanse 2: 1 (stvarno pozitivni: lažni pozitivni rezultati) da pozitivan rezultat testa predstavlja pacijenta s bolešću. Od 3 pozitivna testa, 2 bi se pojavila u bolesnika s bolešću (stvarno pozitivna), a 1 u bolesnika bez bolesti (lažno pozitivno). Budući da su stvarni pozitivni i lažni pozitivni dijelovi izračuna osjetljivosti i specifičnosti, LR +se također može izračunati kao osjetljivost / (1 − specifičnost). Što je LR + veći, to više informacija daje pozitivan rezultat testa; pozitivan rezultat testa s LR+ > 10 smatra se jakim dokazom u korist dijagnoze. Drugim riječima, procjena vjerojatnosti prije ispitivanja snažno se kreće prema 100% kada pozitivni test ima visoki LR +.
Za negativan rezultat testa, LR- od 0,25 pokazuje da su kvote 1:4 (lažno negativi: stvarno negativni) da negativan rezultat testa predstavlja pacijenta s bolešću. Od 5 negativnih rezultata ispitivanja, 1 bi se javio u bolesnika s bolešću (lažno negativan), a 4 kod bolesnika bez bolesti (stvarno negativan). LR- se također može izračunati kao (1 −osjetljivost) / specifičnost. Što je manji LR-, više informacija pruža negativan rezultat testa; negativan rezultat na testu s LR < 0,1 smatra se jakim dokazom protiv dijagnoze. Drugim riječima, procjena vjerojatnosti prije testa kreće se snažno prema 0% vjerojatnosti kada negativni test ima nizak LR-.
Rezultati ispitivanja s LR-om od 1.0 ne sadrže podatke i ne utječu na vjerojatnost bolesti nakon testa
LR su prikladni za usporedbu testova i koriste se u Bayesovoj analizi za tumačenje rezultata ispitivanja. Kako se mijenjaju granične vrijednosti tako se mijenjaju osjetljivost i specifičnost, ali i LR-ovi. Kao hipotetski primjer, visoka vrijednost leukocita (npr. 20 000 /μL) u mogućem slučaju akutne upale slijepog crijeva je specifičniji i imao bi visoki LR+, ali i visoki (i stoga ne baš informativan) LR-; odabir mnogo niže i vrlo osjetljive granične vrijednosti (npr. 10 000 /μL) imao bi nizak LR-, ali i nizak LR+.
Dihotomna ispitivanja
Idealan dihotomni test ne bi imao lažno pozitivne ili lažno negativne; svi bolesnici s pozitivnim rezultatom testa imali bi bolest (100% PPV), a svi bolesnici s negativnim rezultatom testa ne bi imali bolest (100% NPV).
U stvarnosti, svi testovi imaju lažno pozitivne i lažne negativne rezultate, neki testovi više nego drugi. Da biste ilustrirali posljedice nesavršene osjetljivosti i specifičnosti na rezultate ispitivanja, razmislite o hipotetičkim rezultatima (pogledajte tablicu Distribucija rezultata ispitivanja hipotetičkog testa esteraze leukocita u skupini od 1000 žena s pretpostavljenom 30-postotnom prevalencijom UTI-a (upale mokraćnih puteva)) test trakice urina leukocitne esteraze u grupi od 1000 žena, od kojih 300 (30%) ima UTI (što je određeno zlatnim standardnim testom, poput kulture urina). Ovaj scenarij za ilustrativne svrhe pretpostavlja da osjetljivost test trakice ima osjetljivost od 71% i specifičnost od 85%.
Osjetljivost od 71% znači da bi samo 213 (71% od 300) žena s UTI imalo pozitivan rezultat testa. Preostalih 87 imalo bi negativan rezultat testa. Specifičnost 85% znači da 595 (85% od 700) žene bez UTI imalo negativan rezultat testa. Preostalih 105 imalo bi pozitivan rezultat testa. Dakle, od 318 pozitivnih rezultata ispitivanja, samo 213 bi bilo točno (213/318 = 67% PPV); pozitivan rezultat testa čini dijagnozu UTI vjerojatnijom nego nesigurnom, ali ne i sigurnom. Postojala bi i 682 negativna ispitivanja, od kojih 595 točno (595/682 = 87% NPV), što dijagnozu UTI čini mnogo vjerojatnijom, ali ipak mogućom; 13% pacijenata s negativnim rezultatom testa ustvari bi imalo UTI.
Raspodjela rezultata ispitivanja hipotetičkog testa na leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 30% prevalencijom UTI
|
Rezultati
|
Prisutnost bolesti
|
Odsutnost bolesti
|
Ukupno bolesnika
|
|
Pozitivna prediktivna vrijednost (PPV) = SP / (svi bolesnici s pozitivnim testom) = SP / (SP + LP) = 213/(213 + 105) = 67%.
Negativna prediktivna vrijednost (NPV) = SN / (svi bolesnici s negativnim testom) = SN / (SN + LN) = 595/(595 + 87) = 87%.
Pozitivan omjer vjerojatnosti (LR+) = osjetljivost / (1 − specifičnost) =0.71/(1 − 0.85) =4.73.
Negativan omjer vjerojatnosti (LR-) = (1 − osjetljivost) / specifičnost = (1 − 0.71)/0.85 = 0.34.
|
|
Test pozitivan
|
Stvarno pozitivan (SP)
213 bolesnika (71% od 300)
|
Lažno pozitivan (LP)
105 bolesnika (700 −595)
|
318 bolesnika s pozitivnim testom
|
|
Test negativan
|
Lažno negativan (LN)
87 bolesnika (300 −213)
|
Stvarno negativan (SN)
595 bolesnika (85% od 700)
|
682 bolesnika s negativnim testom
|
|
Ukupno bolesnika
|
300 bolesnika s UTI (pretpostavlja se)
|
700 bolesnika bez UTI (pretpostavlja se)
|
1000 bolesnika
|
Međutim, PPV-ovi i NPV-ovi izvedeni u ovoj bolesničkoj skupini ne mogu se koristiti za tumačenje rezultata istog testa kada je osnovna učestalost bolesti (pred-test ili prethodna vjerojatnost) različita. Uočite učinke promjene učestalosti bolesti na 5% (pogledajte tablicu Distribucija rezultata ispitivanja hipotetičkog testa na hipotetsku leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 5% prevalencijom UTI). Sada je većina pozitivnih rezultata ispitivanja lažna, a PPV samo 20%; pacijent s pozitivnim rezultatom testa zapravo ima veću vjerojatnost da nema UTI. Međutim, NPV je sada vrlo visok (98%); negativan rezultat u osnovi isključuje UTI.
Raspodjela rezultata ispitivanja hipotetičkog testa na leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 5% prevalencijom UTI
|
Rezultati
|
Prisutnost bolesti
|
Odsutnost bolesti
|
Ukupno bolesnika
|
|
Pozitivna prediktivna vrijednost (PPV) = SP / (sve s pozitivnim testom) = SP / (SP + LP) = 36/(36 + 144) = 20%.
Negativna prediktivna vrijednost (NPV) = SN / (sve s negativnim testom) = SN / (SN + LN) = 806/(806 + 14) = 98%.
Pozitivan omjer vjerojatnosti (LR+) = osjetljivost / (1 − specifičnost) =0.71/(1 − 0.85) =4.73.
Negativan omjer vjerojatnosti (LR-) = (1 − osjetljivost) / specifičnost = (1 − 0.71)/0.85 = 0.34.
|
|
Test pozitivan
|
Stvarno pozitivni (SP)
36 bolesnika (71% od 50)
|
Lažno pozitivni (LP)
144 bolesnika (950 −806)
|
180 pacijenata s pozitivnim testom
|
|
Test negativan
|
Lažno negativni (LN)
14 pacijenata (50 −36)
|
Stvarno negativni (SN)
806 bolesnika (85% od 950)
|
820 bolesnika s negativnim testom
|
|
Ukupno bolesnika
|
50 bolesnika s UTI (pretpostavlja se)
|
950 bolesnika bez UTI (pretpostavlja se)
|
1000 bolesnika
|
Imajte na umu da se u obje skupine bolesnika, iako su PPV i NPV vrlo različiti, LR-i ne mijenjaju jer se LR određuju samo prema osjetljivosti i specifičnosti ispitivanja.
Jasno, rezultati testa ne daju konačnu dijagnozu, već samo procjenjuju vjerojatnost postojanja ili odsutnosti bolesti, a ta vjerojatnost nakon ispitivanja (vjerojatnost bolesti s obzirom na određeni rezultat testa) uvelike varira ovisno o vjerojatnosti pre testa bolesti kao i osjetljivost i specifičnost testa (a time i njegov LR).
Vjerojatnost pred testiranje
Vjerojatnost pred testiranje nije precizno mjerenje; temelji se na kliničkoj procjeni koliko snažno simptomi i znakovi sugeriraju da je bolest prisutna, koji faktori u anamnezi bolesnika podržavaju dijagnozu i koliko je bolest česta u reprezentativnoj populaciji. Mnogi klinički sustavi bodovanja dizajnirani su za procjenu vjerojatnosti prije ispitivanja; dodavanje bodova za različite kliničke značajke olakšava izračun rezultata. Ovi primjeri ilustriraju važnost točne procjene prevalencije prije testa jer prevalencija bolesti u ispitivanoj populaciji dramatično utječe na korisnost testa. Validirani, objavljeni alati za procjenu prevalencije trebali bi se koristiti kad su dostupni. Na primjer, postoje kriteriji za predviđanje vjerojatnosti plućne embolije prije ispitivanja. Viši izračunati bodovi daju veće procijenjene vjerojatnosti.
Kontinuirana ispitivanja
Mnogi su rezultati ispitivanja kontinuirani i mogu pružiti korisne kliničke informacije o širokom rasponu rezultata. Kliničari često odabiru određenu graničnu vrijednost kako bi maksimizirali korisnost testa. Na primjer, broj leukocita > 15.000 može se okarakterizirati kao pozitivan; vrijednosti < 15.000 kao negativan. Kad test daje kontinuirane rezultate, ali je odabrana određena točka prekida, test funkcionira kao dihotomni test. Također se može odabrati veći broj graničnih vrijednosti. Osjetljivost, specifičnost, PPV, NPV, LR+, i LR- mogu se izračunati za pojedinačne ili veći broj graničnih vrijednosti. Tablica Učinak promjene granične vrijednosti broja leukocita kod bolesnika za koje se sumnja da imaju upalu slijepog crijeva ilustrira učinak promjene granične vrijednosti broja leukocita kod bolesnika za koje se sumnja da imaju upalu slijepog crijeva.
Učinak promjene granične vrijednosti broja leukocita kod bolesnika za koje se sumnja da imaju upalu slijepog crijeva
|
Granična vrijednost leukocita
|
Osjetljivost
|
Specifičnost
|
LR +
|
R-
|
|
* Razne granične vrijednosti su odabrane za kontinuiranu varijablu kao što je broj leukocita; rezultati iznad granične vrijednosti smatraju se pozitivnima i oni ispod granične vrijednosti smatraju se negativnima.
|
|
LR = Omjer vjerojatnosti.
|
|
Adapted from Keskek M, Tez M, Yoldas O, et al: Receiver operating characteristic analysis of leukocyte counts in operations for suspected appendicitis American Journal of Emergency Medicine 26:769–772, 2008.
|
|
> 10,500
|
84%
|
53.13%
|
1.79
|
0.3
|
|
> 11,500
|
78%
|
62.5%
|
2.13
|
0.32
|
|
> 12,850
|
68%
|
75%
|
2.72
|
0.43
|
|
> 13,400
|
61.33%
|
78.12%
|
2.86
|
0.45
|
|
> 14,300
|
56.67%
|
81.25%
|
3.2
|
0.49
|
Alternativno, može biti korisno grupirati kontinuirane rezultate ispitivanja u razine. U ovom slučaju, rezultati se ne okarakteriziraju kao pozitivni ili negativni, jer postoji više mogućih rezultata, pa iako se LR može odrediti za svaku razinu rezultata, više nema zasebnih LR + ili LR-. Na primjer, tablica Korištenje broja leukocita za određivanje koeficijenta vjerojatnosti bakterijemije u febrilnoj djeci ilustrira odnos broja leukocita i bakteremije kod febrilne djece. Budući da je LR vjerojatnost danog rezultata u bolesnika s bolešću podijeljena s vjerojatnošću tog rezultata kod bolesnika bez bolesti, LR za svako grupiranje broja leukocita je vjerojatnost bakterijemije u toj skupini podijeljena s vjerojatnošću da nema bakterijemije.
Korištenje broje leukocita za određivanje koeficijenta vjerojatnosti bakterijemije u febrilnoj djeci *
|
Broj leukocita
|
Broj djece s bakterijemijom, n = 127 (%)
|
Broj djece bez bakterijemije, N = 8629 (%)
|
LR (% S bakterijemijom /% bez bakterijemije)
|
|
* Incidencija bakterijemije kod 8756 febrilne djece grupirane po broju leukocita. LR za svaku skupinu izračunava se dijeljenjem vjerojatnosti bakterijemije s vjerojatnosti da nema bakterijemije.
|
|
LR = Omjer vjerojatnosti.
|
|
Adapted from Lee GM, Harper MB: Risk of bacteremia for febrile young children in the post - Haemophilus influenzae type b era. Archives of Pediatric and Adolescent Medicine 152:624–628, 1998.
|
|
0–5000
|
0 (0.0%)
|
543 (6.3%)
|
0.00
|
|
5,001–10,000
|
3 (2.4%)
|
3291 (38.1%)
|
0.06
|
|
10,001–15,000
|
15 (11.8%)
|
2767 (32.1%)
|
0.37
|
|
15,001–20,000
|
48 (37.8%)
|
1337 (15.5%)
|
2.4
|
|
20,001–25,000
|
34 (26.8%)
|
469 (5.4%)
|
4.9
|
|
25,001–30,000
|
12 (9.4%)
|
155 (1.8%)
|
5.3
|
|
> 30,001
|
15 (11.8%)
|
67 (0.8%)
|
15.2
|
Grupiranje kontinuiranih varijabli omogućuje znatno veću uporabu rezultata ispitivanja nego kad se uspostavi jedna granična vrijednost. Korištenjem Bayesovih analiza, LR-ovi u tablici Korištenje broja leukocita za određivanje koeficijenta vjerojatnosti bakterijemije u febrilnoj djeci mogu se koristiti za izračunavanje vjerojatnosti nakon ispitivanja.
Za kontinuirane rezultate ispitivanja, ako je poznata ROC krivulja, izračuni prikazani u tablici ne moraju se raditi; LR se mogu pronaći za različite točke u rasponu rezultata pomoću nagiba krivulje ROC u željenoj točki.
Bayesov teorem
Postupak korištenja vjerojatnosti bolesti prije ispitivanja i karakteristika ispitivanja za izračunavanje vjerojatnosti nakon testa naziva se Bayesov teorem ili Bayesova revizija. Za rutinsku kliničku upotrebu, Bayesova metodologija obično ima nekoliko oblika:
Izračun vjerojatnosti za slučaj
Ako se vjerojatnost bolesti prije testa izrazi kao vjerojatnost i zato što LR testa predstavlja vjerojatnost, proizvod 2 predstavlja vjerojatnost bolesti nakon testa (analogno množenju 2 vjerojatnosti zajedno kako bi se izračunala vjerojatnost istodobne pojave 2 događaja):
koeficijenti prije testa × LR = koeficijenti poslije testa
Budući da kliničari obično razmišljaju u pogledu vjerojatnosti, a ne šansi, vjerojatnost se pomoću ovih formula može pretvoriti u izglede (i obrnuto):
Izgledi = vjerojatnost / 1 − vjerojatnost
Vjerojatnost = koeficijenti / koeficijenti + 1
Razmotrite primjer UTI kako je dan u tablici Distribucija rezultata ispitivanja hipotetičkog testa na hipotetsku leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 30-postotnom prevalencijom UTI-ja u kojoj je vjerojatnost pre-testa za UTI 0,3, a test kada se koristi, LR + od 4,73 i LR- od 0,34. Vjerojatnost pred testiranje 0,3 odgovara koeficijenta 0,3 / (1 − 0.3) = 0.43. Dakle, izgledi za post-test da je UTI prisutan kod bolesnica s pozitivnim rezultatom testa jednaki su zbroju koeficijenta pred-testa i LR +; 4.73 × 0.43 = 2,03, što predstavlja post-test vjerojatnosti 2,03 / (1 + 2.03) = 0.67. Dakle, Bayesov izračun pokazuje da pozitivan rezultat ispitivanja povećava vjerojatnost pred testiranja s 30% na 67%, isti rezultat dobiven PPV proračunom u tablici.
Sličan je izračun za negativni test; koeficijenti nakon ispitivanja = 0.34 × 0.43 = 0,15, što odgovara vjerojatnosti 0,15 / (1 + 0.15) = 0.13. Dakle, negativan rezultat testa smanjuje vjerojatnost prije ispitivanja s 30% na 13%, što je isti rezultat dobiven izračunavanjem NPV-a u tablici.
Mnogi programi medicinskog kalkulatora koji se izvode na ručnim uređajima dostupni su za izračunavanje vjerojatnosti post-testa od vjerojatnosti pred-testa i LR-a.
Nomogram vjerojatnosti za slučaj
Upotreba nomograma osobito je pogodna jer izbjegava potrebu za pretvaranjem nejednakosti i vjerojatnosti ili stvaranje 2×2 tablica.
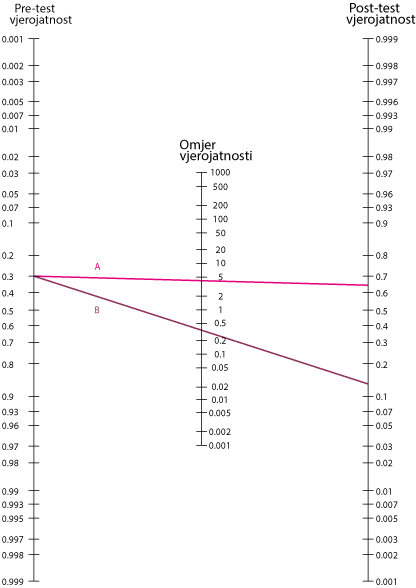
Za korištenje Faganovog nomograma, crta se povlači od pre-test vjerojatnosti do LR. Vjerojatnost post-testa je točka na kojoj ta linija presijeca liniju vjerojatnosti nakon testa. Primjerne crte na slici crtaju se pomoću podataka iz UTI testa u tablici Distribucija rezultata ispitivanja hipotetičkog testa na hipotetsku leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 30% prevalencijom UTI. Red A predstavlja pozitivan rezultat testa; izvodi se iz vjerojatnosti pred testiranja od 0,3 do LR + od 4,73 i daje vrijednost nakon testa neznatno < 0,7, slično izračunatoj vjerojatnosti 0,67. Red B predstavlja negativan rezultat testa; izvodi se iz vjerojatnosti pred-testa od 0,3 do LR- vrijednost 0,34 i daje vrijednost nakon testa neznatno > 0,1, slično izračunatoj vjerojatnosti 13%.
Iako se nomogram čini manje preciznim od izračunavanja, tipične vrijednosti vjerojatnosti pred testiranje često su procjene, pa je prividna preciznost izračuna obično pogrešna.
Faganov nomogram
|
Ilustrativne crte crtaju se pomoću podataka iz UTI testa u tablici Distribucija rezultata ispitivanja hipotetičkog testa na hipotetsku leukocitnu esterazu u skupini od 1000 žena s pretpostavljenom 30% prevalencijom UTI. Linija A predstavlja pozitivan rezultat testa, izvučen iz vjerojatnosti pred testiranje od 0,3 do LR+ od 4,73 do vrijednosti nakon testa od malo < 0,7, slično izračunatoj vjerojatnosti 0,67. Linija B predstavlja negativan rezultat testa izvučen iz vjerojatnosti prije ispitivanja od 0,3 do LR- od 0,34 do vrijednosti nakon testa neznatno > 0,1, slično izračunate vjerojatnosti 13%.
LR+= omjer vjerojatnosti za pozitivan rezultat; LR- = LR za negativan rezultat.
Prilagođeno iz Fagan TJ. Letter: Nomogram for Bayes theorem. New England Journal of Medicine 297:845–850, 1977.
|
Tabelarni pristup
Često LR testa nisu poznati, ali su poznata osjetljivost i specifičnost, pa se može procijeniti vjerojatnost pred testiranja. U ovom se slučaju Bayesova metodologija može provesti korištenjem tablice 2 × 2 ilustrirane u tablici Interpretacija rezultata ispitivanja hipotetičke leukocitne esteraze (LE) korištenjem primjera iz tablice Distribucija rezultata ispitivanja hipotetičkog testa na hipotetsku leukocitu u kohorti 1000 žena s pretpostavljenom 30% prevalencijom UTI. Imajte na umu da ova metoda pokazuje da pozitivan rezultat ispitivanja povećava vjerojatnost UTI-a na 67%, a negativan rezultat smanjuje ga na 13%, isti rezultati dobiveni izračunavanjem pomoću LR-a.
Interpretacija rezultata testa hipotetske leukocitne esteraze (LE) u skupini od 1000 žena koja pretpostavlja 30% prevalenciju UTI (vjerojatnost pre testa), osjetljivost testa 71% i specifičnost 85% *
|
Rezultati
|
UTI prisutan
|
UTI odsutan
|
|
300 bolesnica s UTI
|
700 bolesnica bez UTI
|
|
* Bayesov teorem može se pojednostaviti kako bi se omogućio izračun vjerojatnosti nakon testa kada je poznata vjerojatnost pred testiranja:
-
Post-test vjerojatnosti kad je test pozitivan = TP / (svi s pozitivnim testom) = TP / (TP + FP) = 213/(213 + 105) =67%.
-
Post-test vjerojatnosti kad je test negativan = TN / (svi s negativnim testom) = FN / (FN + TN) = 87/(87 + 595) =13%.
|
|
FN = lažno negativan; FP = lažno pozitivan; TN = stvarno negativan; TP = stvarno pozitivan.
|
|
LE pozitivan test
|
213 bolesnica (TP)
|
105 bolesnica (FP)
|
|
LE negativan test
|
87 bolesnica (FN)
|
595 bolesnica (TN)
|
Sekvencijalno ispitivanje
Kliničari često rade ispitivanja uzastopno tijekom mnogih dijagnostičkih procjena. Ako su koeficijenti pred testom prije uzastopnog ispitivanja poznati i LR za svako ispitivanje u nizu je poznato, kvote za post ispitivanja mogu se izračunati pomoću sljedeće formule:
Pre-test vjerojatnosti × LR1 × LR2 × LR3 = post-test vjerojatnosti
Ova je metoda ograničena važnom pretpostavkom da je svaki od testova uvjetno neovisan.
Testovi probira
Pacijenti često moraju razmisliti trebaju li se pregledati zbog okultne bolesti. Premisa testova probira je da rano otkrivanje poboljšava ishod kod bolesnika s okultnom bolešću i da lažno pozitivni rezultati koji se često pojavljuju kod probira ne stvaraju teret (npr. Troškove i štetne učinke potvrdnog ispitivanja, neopravdano liječenje) koji prelazi takvu korist. Da bi se smanjila ta moguća opterećenja, kliničari moraju odabrati odgovarajući test probira. Test probira nije prikladan kada tretmani nisu učinkoviti ili je bolest vrlo neuobičajena (osim ako se ne može utvrditi podpopulacija u kojoj je prevalencija veća).
Teoretski, najbolji test i za probir i za dijagnozu je onaj s najvećom osjetljivošću i specifičnošću. Međutim, takvi su vrlo točni testovi često složeni, skupi i invazivni (npr. koronarografija) i stoga nisu praktični za probir velikog broja asimptomatskih osoba. Obično se moraju postići određeni kompromisi osjetljivosti, specifičnosti ili oboje prilikom odabira testa probira.
Hoće li kliničar odabrati test koji optimizira osjetljivost ili specifičnost, ovisi o posljedicama lažno pozitivnog ili lažno negativnog rezultata ispitivanja kao i vjerojatnosti pre testa. Idealan test probira je onaj koji je uvijek pozitivan kod gotovo svakog bolesnika s bolešću, tako da negativan rezultat pouzdano isključuje bolest kod zdravih bolesnika. Na primjer, pri testiranju na ozbiljnu bolest za koju je na raspolaganju učinkovito liječenje (npr. koronarna bolest), kliničari će biti voljni tolerirati više lažno pozitivnih nego lažno negativnih (niža specifičnost i visoka osjetljivost). Iako je visoka osjetljivost vrlo važan atribut za testove probira, specifičnost je važna i u određenim strategijama probira. Među populacijom s većom prevalencijom bolesti povećava se PPV probirnog testa; kako se prevalencija smanjuje, post-test ili posteriorna vjerojatnost pozitivnog rezultata opada. Zbog toga se pri probiranju bolesti kod visoko rizične populacije preferiraju testovi s većom osjetljivošću u odnosu na one s većom specifičnošću, jer bolje mogu isključiti bolest (manje je lažno negativnih). S druge strane, u populaciji niskog rizika ili za neuobičajene bolesti za koje terapija ima manju korist ili veći rizik, preferiraju se testovi s većom specifičnošću.
Višestruki testovi probira
Uz sve širi niz dostupnih testova probira, kliničari moraju razmotriti implikacije panela takvih testova. Na primjer, panel testova koji sadrži 8, 12 ili ponekad 20 pretraga krvi često se radi kada je bolesnik tek primljen u bolnicu ili ga liječnik prvi put pregledava. Iako ova vrsta ispitivanja može biti korisna u probiru pacijenata na određene bolesti, korištenje velikog panela testova može imati negativne posljedice. Prema definiciji, test sa specifičnošću od 95% daje lažno pozitivne rezultate kod 5% zdravih, normalnih bolesnika. Ako se rade dva različita ispitivanja s takvim karakteristikama, svaki za različite okultne bolesti, kod bolesnika koji zapravo nema nijednu bolest, vjerojatnost da će oba ispitivanja biti negativna je 95% × 95% ili oko 90%; dakle, postoji 10% šanse za barem jedan lažno pozitivan rezultat. Za tri takva ispitivanja, vjerojatnost da bi sva tri bila negativna je 95% × 95% ×95% ili 86%, što odgovara 14% šansi za barem jedan lažno pozitivan rezultat. Ako se napravi 12 različitih ispitivanja na 12 različitih bolesti, šansa za dobivanje barem jednog lažno pozitivnog rezultata je 46%. Ova velika vjerojatnost naglašava potrebu za oprezom prilikom odlučivanja o korištenju testova probira i prilikom tumačenja njegovih rezultata.
Ispitivanje pragova
Laboratorijsko testiranje se treba obaviti samo ako njegovi rezultati utječu na odlučivanje; inače su trošak i rizik za bolesnika ništavni. Kliničari ponekad mogu odrediti vrijeme testiranja uspoređujući procjene vjerojatnosti pre testa i post testa s određenim pragovima. Iznad određenog praga vjerojatnosti, koristi liječenja nadmašuju rizike (uključujući rizik pogrešnog liječenja pacijenta bez bolesti), a liječenje je indicirano. Ta se točka naziva pragom liječenja i određuje se kako je opisano u Kliničkim strategijama donošenja odluka: procjene vjerojatnosti i prag liječenja. Po definiciji, ispitivanje je nepotrebno kada je vjerojatnost pred testiranja već iznad praga liječenja. Ali ispitivanje je indicirano ako je vjerojatnost pred testiranja ispod praga liječenja sve dok pozitivni rezultati ispitivanja mogu povećati vjerojatnost post-testa iznad praga liječenja. Najniža vjerojatnost pred testiranja kod koje se to može dogoditi ovisi o karakteristikama ispitivanja (npr. LR +) i naziva se ispitnim pragom.
Konceptualno, ako najbolji test za ozbiljan poremećaj ima nizak LR +, a prag liječenja je visok, razumljivo je da pozitivan rezultat testa ne bi pomaknuo vjerojatnost post-testa iznad praga liječenja kod pacijenta s niskim, ali zabrinjavajućom vjerojatnosti pred testiranja (npr. možda 10% ili 20%).
Za numeričku ilustraciju razmotrite prethodno opisani slučaj mogućeg akutnog infarkta miokarda u kojem je ravnoteža između rizika i koristi odredila prag liječenja od 25%. Kada vjerojatnost infarkta miokarda prelazi 25%, daje se trombolitička terapija. Kada treba napraviti brzi ehokardiogram prije davanja trombolitičke terapije? Pretpostavimo hipotetsku osjetljivost od 60% i specifičnost od 70% za ehokardiografiju u dijagnosticiranju infarkta miokarda; ovi postoci odgovaraju LR + 60 / (100 − 70) = 2 i LR- za (100 −60)/70 = 0.57.
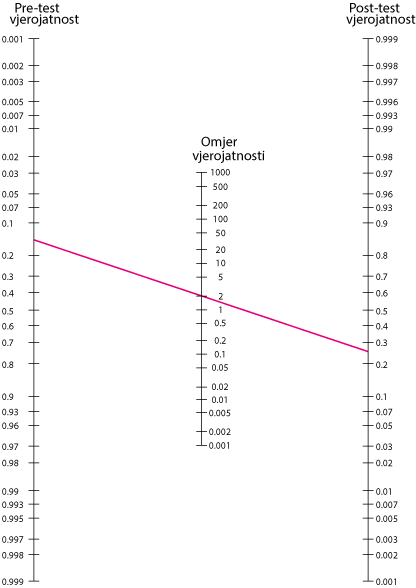
Pitanje se može riješiti matematički (koeficijenti prije testiranja × LR = izgledi post-testa) ili intuitivnije grafički pomoću Faganovog nomograma. Na nomogramu, linija koja povezuje prag liječenja (25%) na liniji vjerojatnosti nakon testa kroz LR + (2.0) na srednjoj LR liniji presijeca vjerojatnost prije ispitivanja od oko 0,14. Jasno, pozitivan test kod pacijenta s bilo kojom vjerojatnošću pre testa < 14% i dalje će rezultirati vjerojatnošću post-testa manjom od praga liječenja. U ovom slučaju ehokardiografija bi bila beskorisna jer čak i pozitivan rezultat ne bi doveo do odluke o liječenju; prema tome, 14% vjerojatnosti pred testiranje je prag ispitivanja za ovaj određeni test (vidi sliku Prikazivanje pragova ispitivanja i liječenja). Drugi test s različitim LR + imao bi različit prag ispitivanja.
Faganov nomogram kojim se određuje potreba za ispitivanjem.
|
U ovom primjeru, pretpostavlja se da pacijent ima prag liječenja (TT) od 25% za akutni infarkt miokarda. Kada vjerojatnost infarkta miokarda prelazi 25%, daje se trombolitička terapija. Kliničari mogu pomoću Faganovog nomograma odrediti kada treba učiniti brzu ehokardiografiju prije davanja trombolitičke terapije. Pod pretpostavkom da ehokardiografija ima hipotetičku osjetljivost od 60% i specifičnost od 70% za novi MI, ti postoci odgovaraju omjeru vjerojatnosti (LR) pozitivnog rezultata ispitivanja (LR+) od 60 / (100 − 70) = 2. Linija koja povezuje prag od 25% obrade na liniji vjerojatnosti nakon ispitivanja s LR + (2.0) na srednjoj LR liniji presijeca vjerojatnost prije ispitivanja od oko 0,14. Pozitivan rezultat testa kod pacijenta s vjerojatnosti pre testa < 14% i dalje rezultira u vjerojatnosti post-testa manjoj od praga liječenja.
Prilagođeno iz Fagan TJ. Letter: Nomogram for Bayes theorem. New England Journal of Medicine 297:845–850, 1977.
|
Prikaz pragova ispitivanja i liječenja.
|
Vodoravna linija predstavlja vjerojatnost nakon ispitivanja.

|
Budući da 14% i dalje predstavlja značajan rizik od infarkta miokarda, jasno je da vjerojatnost bolesti ispod ispitnog praga (npr. 10% vjerojatnost pred testiranje) ne znači nužno da je bolest isključena, već samo da pozitivan rezultat testa na određeni test u pitanju ne bi mijenjao način liječenja i samim tim taj test nije naveden. U ovoj situaciji, liječnik će promatrati bolesnika radi daljnjih nalaza koji bi mogli povećati vjerojatnost pred testiranje iznad praga ispitivanja. U praksi, je za određenu bolest često dostupno više testova, te se može upotrijebiti sekvencijalno ispitivanje.
Ovaj primjer smatra da test sam po sebi ne predstavlja rizik za bolesnika. Ako test ima ozbiljne rizike (npr. kateterizacija srca), prag testiranja trebao bi biti viši; kvantitativni proračuni se mogu napraviti, ali su složeni. Stoga, smanjivanje osjetljivosti i specifičnosti testa ili povećanje njegovog rizika sužava raspon vjerojatnosti bolesti nad kojima je testiranje najbolja strategija. Poboljšanje sposobnosti testa da diskriminira ili smanji rizik širi raspon vjerojatnosti nad kojima je testiranje najbolja strategija.
Moguća iznimka od propisa protiv testiranja je kada je vjerojatnost pred testiranja ispod praga ispitivanja (ali je još uvijek zabrinjavajuća) može biti ako negativni rezultati testa mogu smanjiti vjerojatnost posta-testa ispod točke u kojoj se može smatrati da se bolest može isključiti. Ovo određivanje zahtijeva subjektivnu procjenu stupnja sigurnosti potrebnog da bi se isključila bolest i, s obzirom na to da su u to uključene male vjerojatnosti, posebna pažnja posvećena bilo kakvim rizicima testiranja.